Hi Haasoscope fans!

Thanks to your support we’ve already reached 90% funded, with 2 weeks still left to go! Please post / tweet / share, to spread the word, and help get this project funded.

The prototype is very advanced now - take a look at the latest board I just sent to the fab:

I’ve also spent some time last week working on a quite new use for the Haasoscope - thanks to an idea from a fellow professor here at NYU - a lock in amplifier. The idea is to measure the phase and amplitude of an input signal, with respect to a reference signal. You can read more about lock-in’s here: https://en.wikipedia.org/wiki/Lock-in_amplifier

A standard lock in usually goes for ~$5,000, but the Haasoscope can do a pretty good job of it!

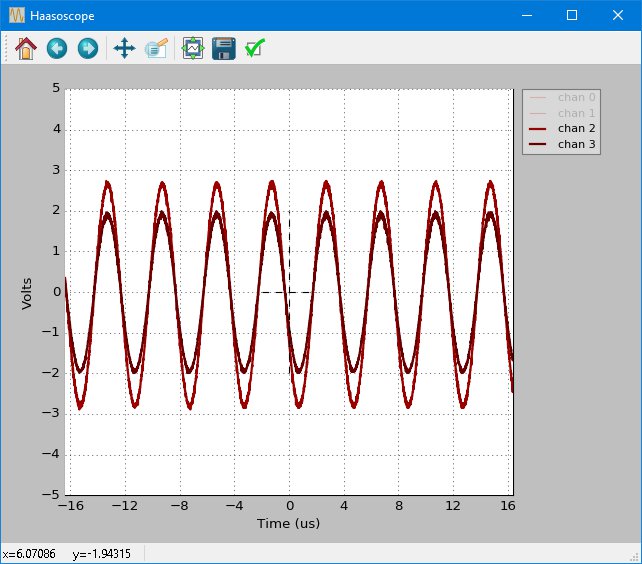
For instance, here’s two 250 kHz sine waves, from ch1 and ch2 of my signal generator, as seen by the Haasoscope:

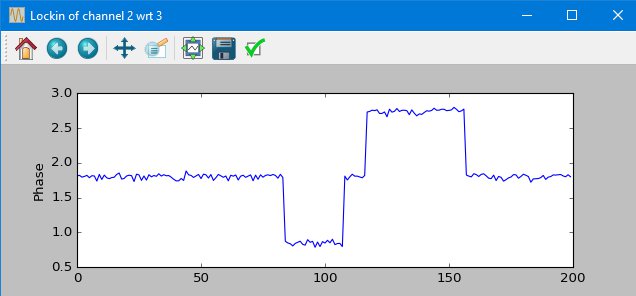
If you were to shift one of those waves to the right or left, that’s changing the relative phase of the waves. This could happen, for instance, by having a longer path one signal needs to take, by going through a material with a larger index of refraction, or whatever. I’ve implemented the lockin calculation, which basically multiplies the two waves together, like vectors. (It also multiplies it by the reference wave shifted by 90 deg, to get the distance on the imaginary axis.) Here’s a plot from the Haasoscope software of adjusting the phase by just +- 1 degree:

It’s so sensitive I can even tell that one of my BNC cables is 6’ longer than the other! (The phase is offset by ~1 deg. 6’ is about 12 ns, since the signal travels at about c/2 in a BNC cable. And a phase of 1 deg for 250 kHz is 4000 ns / 360 = ~11 ns.)

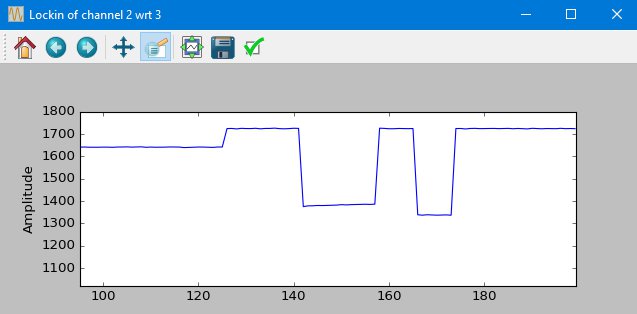
It also calculates the amplitude of the wave relative to the reference wave - so signals of the same frequency have large amplitude, but those of other frequencies have small amplitude. This is where the "lock in" amplifier gets its name - it only gives large amplitude for signals that have the same frequency as the reference signal (or very close to it). It’s like a very narrow bandpass filter. Here’s a plot from the Haasoscope of varying the signal by just 0.1kHz, vs the 250 kHz reference:

Even frequencies that differ from the reference by just ~0.1% have much lower amplitude. And by 0.5% difference from the reference they have nearly zero amplitude.

Now doing all this offline in python would is easy, but it’s slow! You have to read out all those samples (256kb!) for each measurement, so at most you could measure the phase a few times per second, and you’d burn a hole through your CPU! But the Haasoscope can easily calculate the phase and amplitude in the FPGA, so you just have to read out the calculated phase and amplitude, which is 16 bits. It can thus measure the phase and amplitude about 500 times per second, with no CPU!

The professor I mentioned above is interested in using this to measure an acoustic hologram. I’m not totally sure what that means yet either - but the idea is basically to detect and move 3D objects by measuring with a microphone how the phase of a reference sound from a speaker is modified by an object, due to different speed of sound in the object vs air. And the lock-in will only hear frequencies very close to the reference frequency, so ambient noise will have little effect, since it’s at many frequencies!

Here’s a video of what you can do with these things: https://youtu.be/s5r2nmvxA4s

Neat!